N <- 100
p <- sapply(1:(N-1), function(m) m/N*sum(1/seq(m, N-1)))
plot(1:(N-1), p, type="l")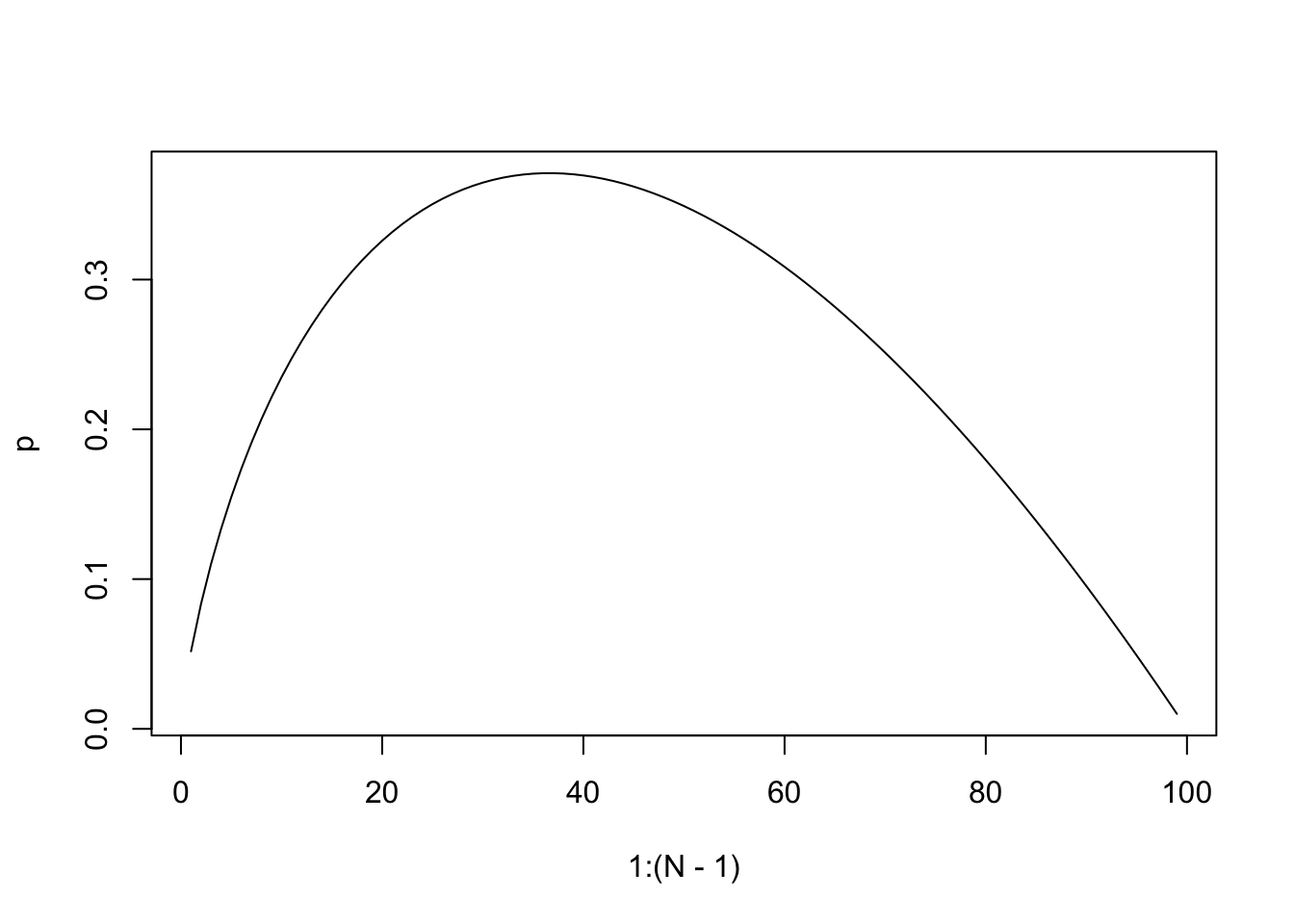
The question
How many people should you date before you settle down with someone for marriage? The answer is you should date 37% of your potential options and choose the next one who is better. 1
The 37% Rule, also known as the Optimal Stopping Theory, provides a strategy to maximize the chances of making the best choice when faced with a sequence of options where decisions are irreversible. It suggests that you should review and reject the first 37% of the total options without selecting any, then choose the next option that is better than all those previously considered.
Mathematical framework
Let’s assume there’s a pool of \(N\) people out there from which you are choosing. We’ll also assume that you have a clear-cut way of rating people. You know who is the best to be your partner. We will call that person Mr/Ms \(X\). The people that you will meet show up one by one in random order. \(X\) may show up anywhere in the sequence. Sadly, a person you have dated and then rejected isn’t available to you any longer later on. So you cannot date all of them and pick the best one.
Your dating strategy is to date \(M\) of the \(N\) people and then settle with the next person who is better. Our task is to find the optimal \(M\). If \(M\) is too small, you will likely land with someone before \(X\) shows up. If \(M\) is too large, \(X\) will likely pass \(X\) and pick someone less optimal. Of course, there is no perfect solution. We want to find the \(M\) that maximizes the probability of landing \(X\).
Let \(P(M,N)\) be the probability of successfully picking \(X\) if you date \(M\) people out of \(N\) and then go for the next person who is better than the previous ones. Let \(S\) be the event of successfully picking \(X\), and \(X_j\) means \(X\) is in the \(j\)th position in the sequence. The overall probability is: \[P(M,N) = P(S|X_1)P(X_1)+P(S|X_2)P(X_2)+\cdots+P(S|X_n)P(X_n)\]
For a given value of \(M\), if \(X\) is among the first \(M\) people you date, then you have missed your chance. The probability of settling with \(X\) is zero. Therefore, the first \(M\) terms are all zero.
If \(X\) is in \(M+1\), you’re in luck: since \(X\) is better than all others so far, you will pick \(X\) for sure. Therefore, \[P(S|X_{M+1})P(X_{M+1}) = 1\cdot P(X_{M+1})= \frac{1}{N}\] Since \(X\) is equally likely to be in any position, the probability of \(X\) being in \(M+1\) out of \(N\) people is \(1/N\).
If \(X\) is in \(M+2\), you’ll pick him/her up as long as the \((M+1)\)st person didn’t have a higher rating than all the previous \(M\) people. In other words, you would pass the \((M+1)\)st person and pick \(X\) if the best one out of the \((M+1)\) people has shown up among the first \(M\) people. The change is \(M/(M+1)\). Thus, \[ P(S|X_{M+2})P(X_{M+2})=\frac{M}{M+1}\frac{1}{N} \]
Similarly, if \(X\) shows up in \(M+3\), you’ll pick him/her up to as long as neither the \((M+1)\)st nor the \((M+2)\)nd person have a higher rating than all the previous \(M\) people. In other words, the best one out of the first \((M+2)\) people has to show up among the first \(M\) people. The chance is \(M/(M+2)\). Thus,
\[ P(S|X_{M+3})P(X_{M+3})=\frac{M}{M+2}\frac{1}{N} \]
Putting them all together, we have \[ \begin{aligned} P(M,N) &=\frac{1}{N} +\frac{M}{N(M+1)} +\frac{M}{N(M+2)}+\dots +\frac{M}{N(N-1)}\\ &= \frac{M}{N}\left(\frac{1}{M}+\frac{1}{M+1} +\frac{1}{M+2}+\dots+\frac{1}{N-1}\right) \end{aligned} \]
Maximizing your chance of success
Assuming \(P(M,N)\) is strictly concave (fortunately this is the case), the \(M\) the maximizes the chance satisfies \[ P(M-1,N) < P(M,N) \text{ and } P(M+1,N) < P(M,N) \]
We can ask the computer to find the solution:
N <- 100
p <- sapply(1:(N-1), function(m) m/N*sum(1/seq(m, N-1)))
plot(1:(N-1), p, type="l")
For \(N=100\), the highest probability if achieved at \(M=37\).
The limiting solution
We can find the solution analytically if \(M,N\) are large. For large \(n\), the harmonic sequence can be approximated by the logarithm function: \[ H_n=1+\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n}\approx \ln(n)+\gamma \] where \(\gamma\) is a constant.
We rewrite the function \(P(M,N)\) as \[ P(M,N) =\sum_{k=M}^{N-1}\frac{M}{N}\cdot\frac{1}{k} =\frac{M}{N}\sum_{k=M}^{N-1}\frac{1}{k} =\frac{M}{N}\Big(H_{N-1}-H_{M-1}\Big) \]
For large \(M\) and \(N\), it is approximated by \[ P(M,N)=\frac{M}{N}(H_{N-1}-H_{M-1})\approx \frac{M}{N}\left[\ln(N-1)-\ln(M-1)\right]\approx \frac{M}{N}\ln\left(\frac{N}{M}\right) \]
Let \(x=\frac{M}{N}\in(0,1)\). We want to maximize \[ f(x)=x\ln\left(\frac{1}{x}\right)= -x\ln x \]
Differentiate: \[ f'(x)=\ln\left(\frac{1}{x}\right)-1=-\ln x -1 \]
Set \(f'(x)=0 \Rightarrow -\ln x -1=0 \Rightarrow \ln x=-1 \Rightarrow x=e^{-1}.\) Second derivative \(f''(x)=-1/x<0\), so it’s a maximum.
Therefore, the maximizing fraction satisfies \[ \frac{M^\star}{N}\;\longrightarrow\;\frac{1}{e}\quad\text{as }N\to\infty, \]
and the maximal success probability tends to \[ f(1/e)=\frac{1}{e}. \]
See Kissing the frog: A mathematician’s guide to mating and Strategic dating: The 37% rule for reference.↩︎