39  Portfolio allocation*

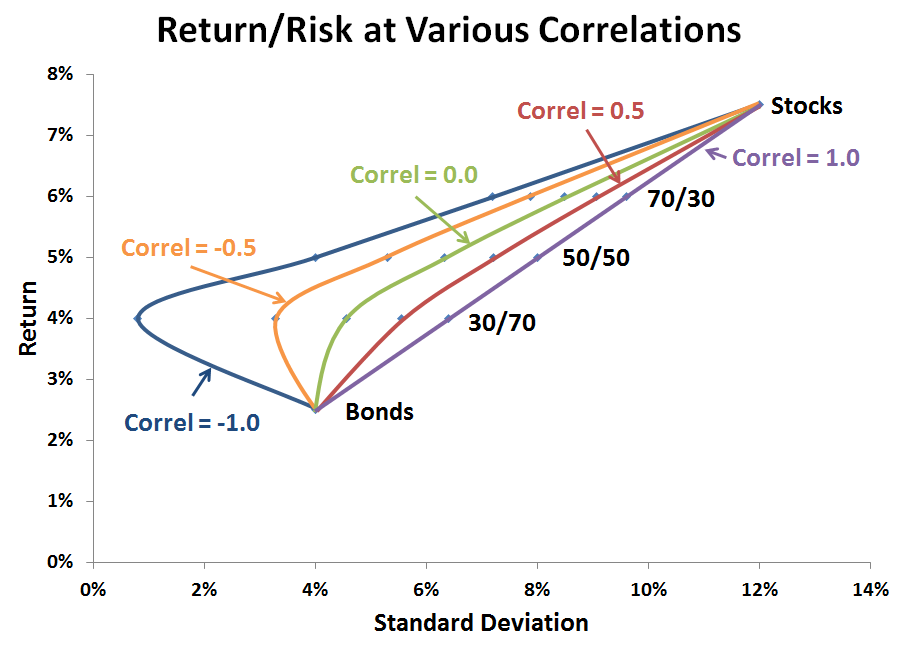
In the world of finance, one of the most well-established principles is the idea of diversification. By combining assets with varying levels of risk and return, investors can reduce the overall risk of their portfolio.

Consider a portfolio of two assets, Asset A and Asset B. Both assets have the same expected return and individual risks (standard deviations), and they are weighted equally in the portfolio.

Asset	Return \(\mu\)	Risk \(\sigma\)	Weight \(w\)
A	10%	15%	50%
B	10%	15%	50%

The expected return of the portfolio is: \[\mu_P=w_A\mu_A + w_B\mu_B = 10\%\] Let’s consider the portfolio risk. First, assuming high correlation, \(\rho_{AB}^H=0.8\). The portfolio risk is: \[\sigma_P^{H} = \sqrt{w_A^2 \sigma_A^2 + w_B^2 \sigma_B^2 + 2w_A w_B \sigma_A \sigma_B \rho_{AB}^H}\approx 14.2\%\]

If assuming low correlation, \(\rho_{AB}^L=0.2\). The portfolio risk is: \[\sigma_P^{L} = \sqrt{w_A^2 \sigma_A^2 + w_B^2 \sigma_B^2 + 2w_A w_B \sigma_A \sigma_B \rho_{AB}^L}\approx 11.6\%\]

As we see, by reducing the correlation between the two assets, we reduced the portfolio risk, though the expected return remains the same. Therefore, diversification is often referred to as a “free lunch” in finance because it allows investors to reduce portfolio risk without sacrificing expected returns.