18 Cumulative distribution

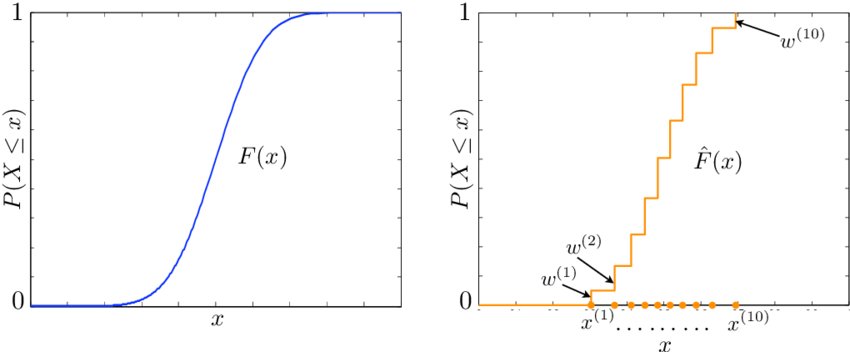
Definition 18.1 (Cumulative distribution function) The cumulative distribution function (CDF) of a random variable \(X\) is the function \(F\) given by \(F(x)=P(X\leq x)\).

For discrete random variables, \(F(x)=\sum_{k\leq x}p(k)\).

For continuous random variables, \(F(x)=\int_{-\infty}^{x}f(t)dt\). We thus have \(\frac{dF(x)}{dx}=f(x)\).

Unlike PMF or PDF, a cumulative distribution function can be defined for both discrete and continuous random variables. CDF gives the full distribution of a random variable. Given the CDF, we can figure out any probability distribution of the random variable: \[P(x_{1}<x\leq x_{2})=F(x_{2})-F(x_{1}).\]

Proposition 18.1 Any CDF has the following properties:

\(P(X>x)=1-F(x)\)
\(P(x_{1}<x\leq x_{2})=F(x_{2})-F(x_{1})\)
Increasing: if \(x_{1}\leq x_{2}\), then \(F(x_{1})\leq F(x_{2})\).
Right-continuous: for any \(a\), \(F(a)=\lim_{x\to a+}F(x)\).
\(F(x)\to0\) as \(x\to-\infty\); \(F(x)\to1\) as \(x\to+\infty\).

The CDF for a continuous random variable is differentiable, while the CDF for a discrete random variable consists of jumps and ﬂat regions.