22  Geometric distribution

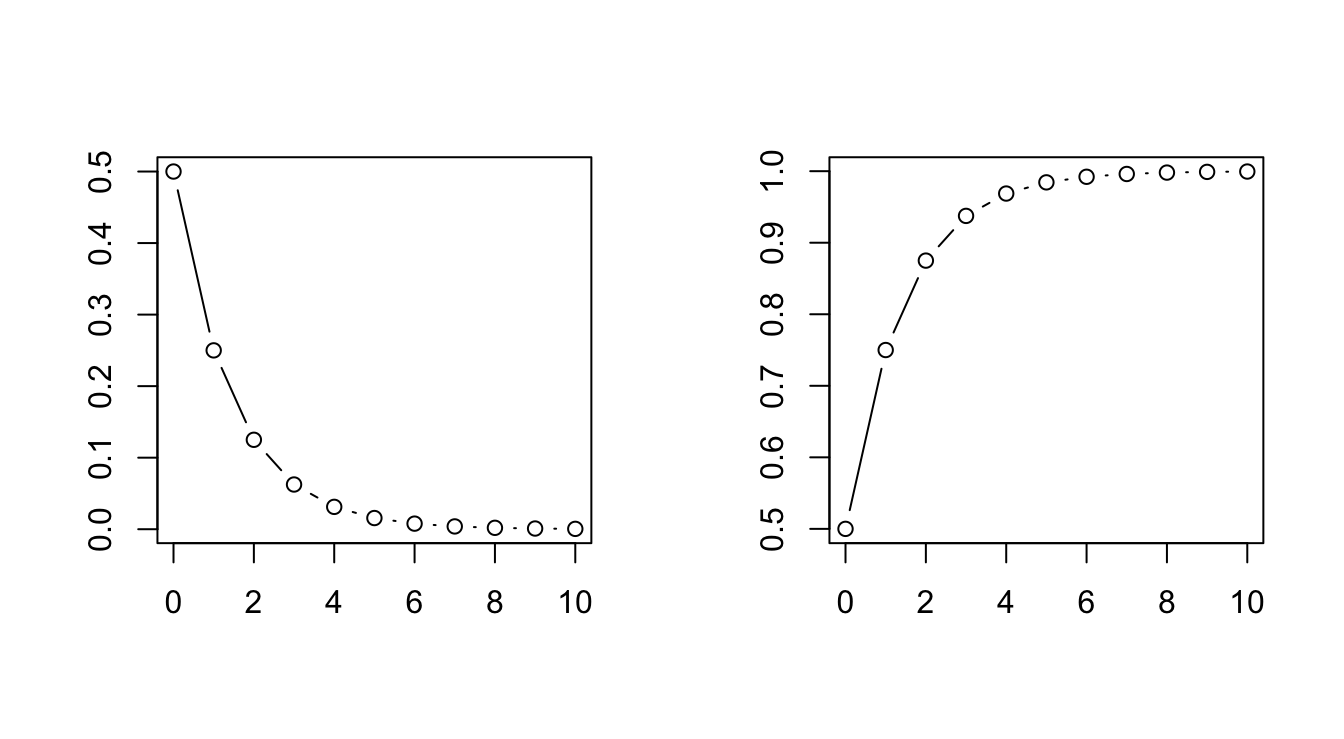
Definition 22.1 (Geometric distribution) Consider a sequence of independent Bernoulli trials, each with the same success probability \(p\). Let \(X\) be the number of failures before the first successful trial. Then \(X\) has a Geometric distribution: \(X\sim\textrm{Geom}(p)\).

Let’s derive the PMF for the Geometric distribution. By definition,

\[P(X=k)=q^{k}p\] where \(q=1-p\). This is a valid PMF because \[\sum_{k=0}^{\infty}q^{k}p=p\sum_{k=0}^{\infty}q^{k}=\frac{p}{1-q}=1.\] The expectation of \(X\) is given by

\[E(X)=\sum_{k=0}^{\infty}k\cdot q^{k}p=p\sum_{k=0}^{\infty}kq^{k}=p\frac{q}{p^{2}}=\frac{q}{p}.\] To see why this holds, taking derivative with respect to \(q\) on both sides of \(\sum_{k=0}^{\infty}q^{k}=\frac{1}{1-q}\) yields

\[\sum_{k=1}^{\infty}kq^{k-1}=\frac{1}{(1-q)^{2}};\] Then multiply both sides by \(q\):

\[\sum_{k=1}^{\infty}kq^{k}=\frac{q}{(1-q)^{2}}=\frac{q}{p^{2}}.\]

Plot the PMF and CDF

par(mfrow=c(1,2))

# PMF for Geom(0.5)
curve(dgeom(x, 0.5), from=0, to=10, n=11, type="b", ann=F)

# CDF for Geom(0.5)
curve(pgeom(x, 0.5), from=0, to=10, n=11, type="b", ann=F)

Example 22.1 (Coin flip until Head) Flipping a fair coin, what is the expected number of flips before the first Head?

Let \(X\) be the number of flips until the first head. We know \(X-1\sim\text{Geom}(0.5)\) as geometric distribution models the number of failures excluding the success. Thus, \(E(X-1)=0.5/0.5=1\), \(E(X)=2\). Let’s compare the theoretical value with results from simulations.

# number of simulations
N <- 1000  

# X: number of flips until first head
# stores value of X in each simulation
X <- numeric(N) 

set.seed(100)

# run simulations
for (i in 1:N) {
  x <- 0
  # repeat until first head
  while(TRUE) {
    x <- x + 1
    t <- sample(c('H','T'), 1, F)
    if (t == 'H') break
  }
  # record the number
  X[i] <- x
}

# plot distribution of X
hist(X, probability=T)

#overlay with geometric distribution
curve(dgeom(x-1,.5), from=1, to=10,n=10,add=T,col=2)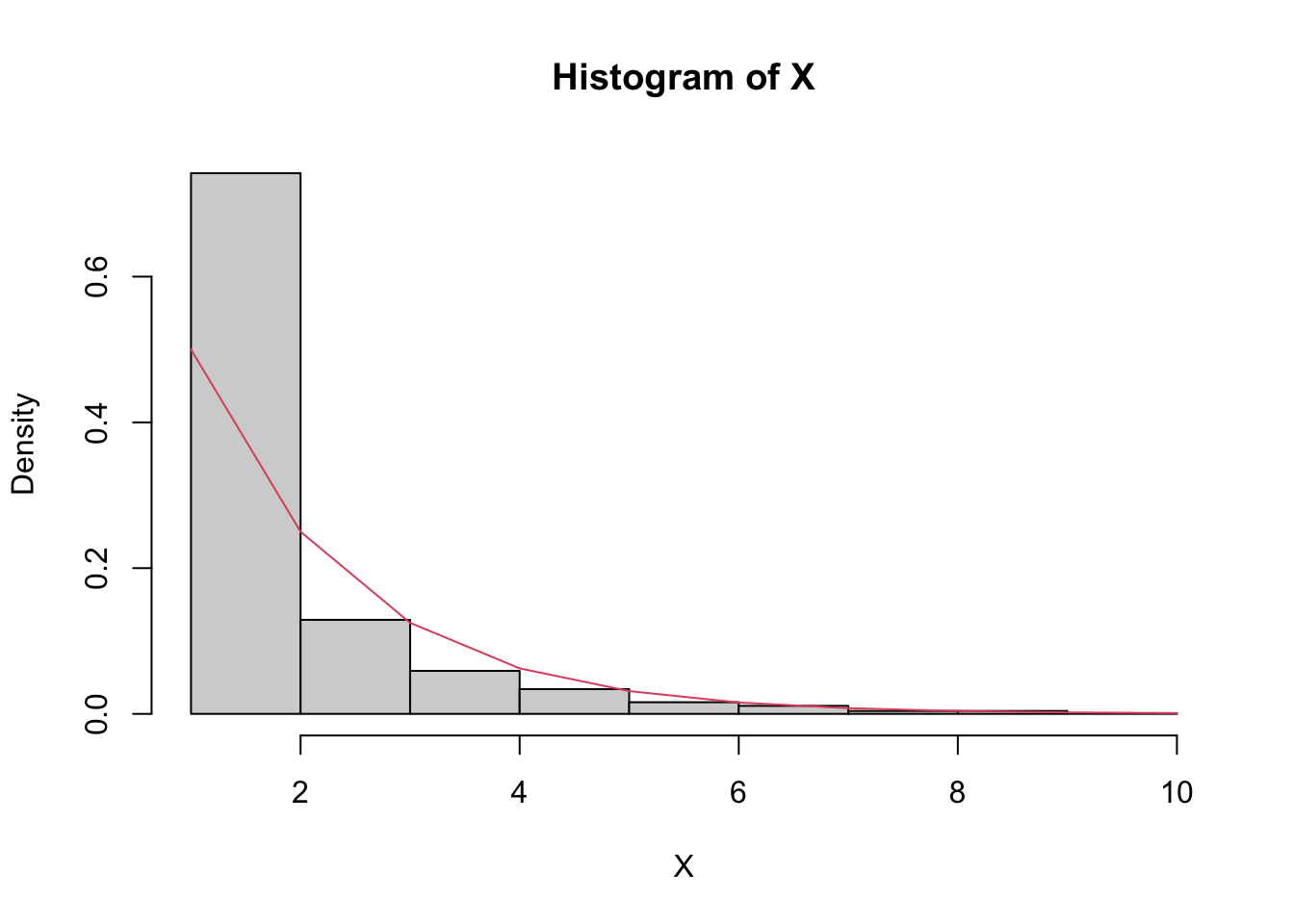

cat("Average number of flips until Head:", mean(X))

Average number of flips until Head: 2.021