library(lattice) # easy to make conditional plots
# conditional distribution of exam scores
exam <- read.csv("../dataset/exam.csv")
# distribution of exam scores conditioned on major
histogram(~ final | major, data = exam)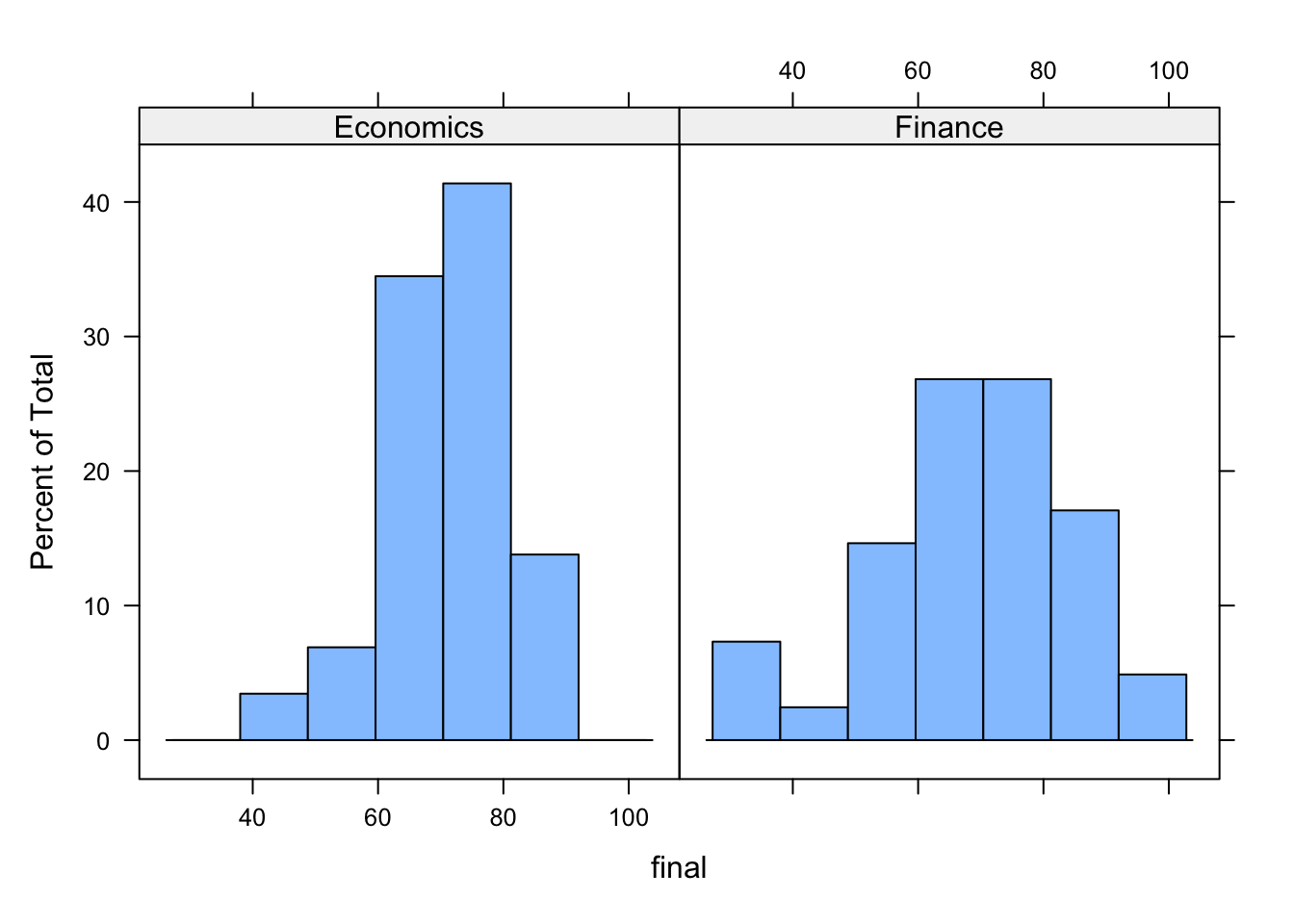
26 Conditional distribution
Definition 26.1 (Conditional distribution) The conditional PMF of \(Y\) given \(X=x\) is defined as \[f_{Y|X} (y|x) = P(Y=y | X=x)=\frac{P(Y=y,X=x)}{P(X=x)}\] for any \(x\) such that \(P(X=x)>0\).
Plot conditional distribution
Definition 26.2 (Conditional expectation) The conditional expectation of \(Y\) given \(X=x\) is defined as \[\psi(x) = E(Y|X=x)= \sum_{\text{all }y} y\ f_{Y|X}(y|x).\] \(\psi(x)\) depends on the value of \(x\) taken by \(X\), so it can be thought of as a function \(\psi(X)\) of \(X\) itself. \[\psi(X)= E(Y|X)\] is called the conditional expectation of \(Y\) given \(X\).
Note
Although \(E(X)\) is a number, \(E(Y|X)\) is a random variable. It is a function of random variable \(X\), and therefore it is a random variable itself.
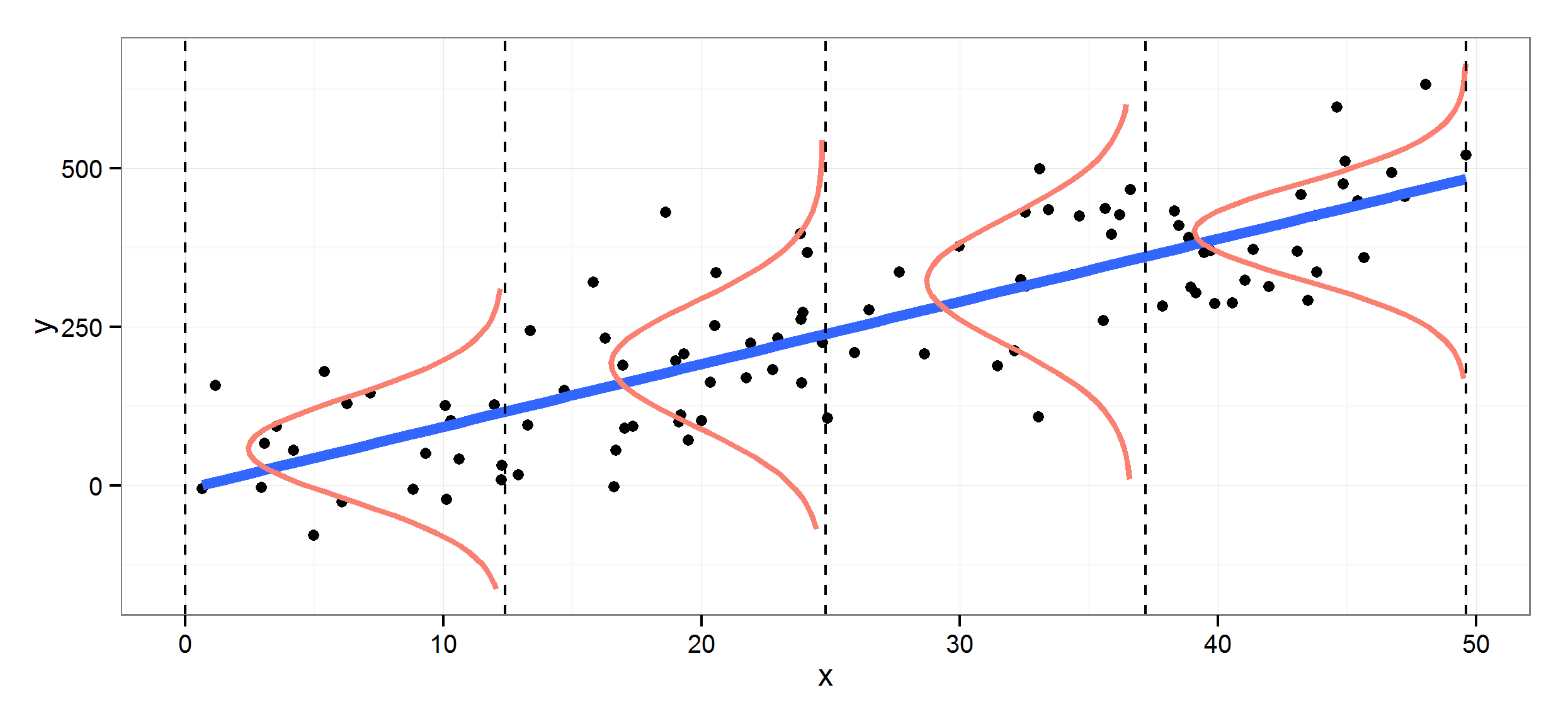
Conditional distribution is a key concept in probability, describing how the distribution of one random variable depends on the values of other variables—an idea central to many practical applications. For instance, we might be interested in how income distributions vary by education level or how the probability of a disease changes with age.
Conditional expectation gives the expected value of one variable given the value of another. It is frequently used for making predictions, such as predicting your earnings given that you graduate from a this college.
